다익스트라 알고리즘은 음의 간선이 없을 때 사용할 수 있는 하나의 정점에서 다른 모드 정점으로 가는 최단 경로를 구할 때 사용하는 알고리즘이에요. 현실 세계에선 음의 간선이 없기 때문에 현실세계에서도 사용하기 적합한 알고리즘 중 하나예요.
다익스트라 알고리즘은 시작 노드부터 인접노드들을 방문하며 최단 거리를 구할 때 이전에 구했던 최단 거리 정보를 재사용하는 특징이 있어요. 이때 인접노드가 여러 개가 있다면 가장 낮은 cost를 갖는 노드부터 방문하며 cost를 갱신하게 구현해 봤어요.
구현해야 하는 내용들은 다음과 같아요.
1. 출발 노드 세팅.
2. 출발 노드를 기준으로 각 노드의 최소 비용을 세팅.
3. 방문하지 않는 노드 중 가장 cost가 적은 노드 선택.
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신.
5. 3 ~ 4 반복
아래와 같은 그래프가 있다고 생각하고 진행해 볼게요.

1. 출발 노드는 1번 노드부터 한다고 가정했어요.
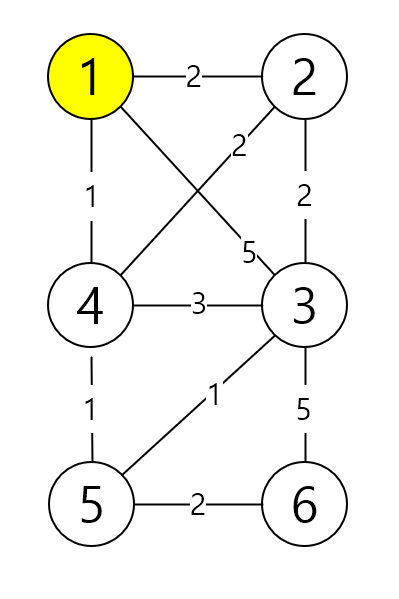
2. 출발노드를 기준으로 각 노드의 최소비용을 세팅해요.
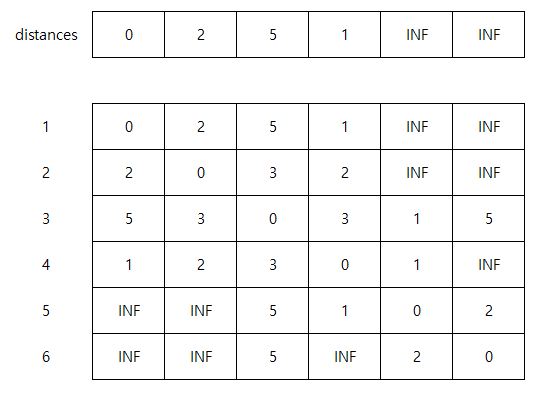
현재 1번 노드는 2, 3, 4 하고만 연결이 되어 있기 때문에 다음과 같은 값을 갖고 있어요.
이 중 에서 이제 4번 노드의 cost가 가장 낮기 때문에 4번 노드부터 탐색합니다.
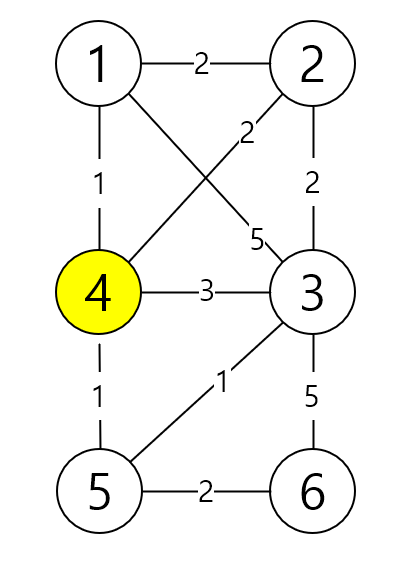

4번 노드에서 갈 수 있는 노드들은 1, 2, 3, 5번 노드가 있어요.
이것들을 1번에서 4번까지 가는 cost(1) + 각 노드까지 가는 cost가 기존에 등록되어 있는 값들보다 저렴하게 갈 수 있는지를 체크하는 거예요.
1번 노드 1 + 1 < 0 X
2번 노드 1 + 2 < 2 X
3번 노드 1 + 3 < 5 O
5번 노드 1 + 1 < INF O
다음과 같이 더 낮은 값이 있으면 distances를 갱신해 줘요.

방문 한 노드는 파란색으로 표현할게요
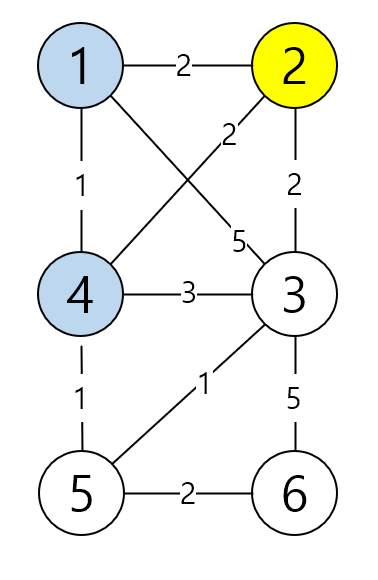
이제 방문 안 한 노드 중 가장 낮은 cost값을

갖는 노드는 2번과 5번이 있는데 이때는 앞에 인덱스부터 찾아요.
2번은 1, 3, 4 노드랑 연결이 되어 있네요.
1번 노드 2 + 2 < 0 X
3번 노드 2 + 2 < 2 X
4번 노드 2 + 2 < 1 X
갱신되는 노드가 없네요.

이제 5번 노드를 탐색해요.
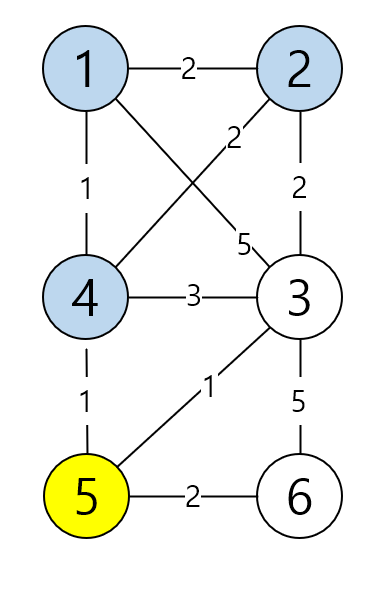

5번 노드는 3, 4, 6 하고 연결이 되어 있네요.
3번 노드 2 + 1 < 4 O
4번 노드 2 + 1 < 1 X
6번 노드 2 + 2 < INF O
3, 6번 노드가 갱신이 일어났어요.

마찬가지로 3번과 6번 노드의 cost값이 같기 때문에 3번 노드부터 탐색을 해요.
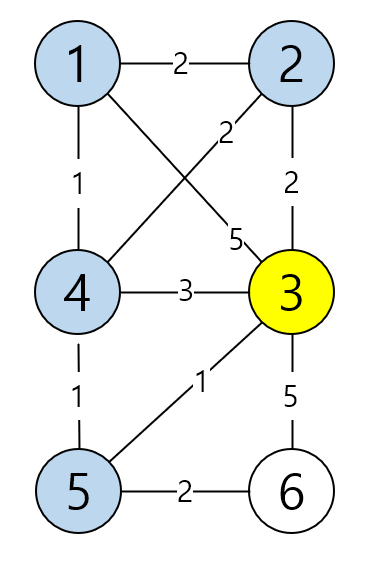

3번 노드는 1, 2, 4, 5, 6 하고 연결이 되어 있네요. 모든 노드하고 연결이 되어 있어요.
1번 노드 3 + 5 < 0 X
2번 노드 3 + 2 < 2 X
4번 노드 3 + 3 < 1 X
5번 노드 3 + 1 < 2 X
6번 노드 3 + 5 < 4 X

갱신되는 노드가 없네요.


마지막 6번 노드는 3, 5 하고 연결이 되어 있네요.
3번 노드 4 + 5 < 0 X
5번 노드 4 + 2 < 2 X

이렇게 모든 노드 방문이 끝나면 1번 노드에서 각 노드까지 가는 최적의 cost를 구할 수 있어요.
#define INF 1000000000
#include <iostream>
#include <vector>
using namespace std;
int V, E;
int startIndex;
vector <pair<int, int>> graph[7];
int distances[7];
bool visit[7];
// 가장 최소 cost를 가지는 정점을 반환합니다.
int GetSmallIndex()
{
int min = INF;
int index = 0;
for (int i = 1; i <= V; i++)
{
if (distances[i] < min && !visit[i])
{
min = distances[i];
index = i;
}
}
return index;
}
void Dijkstra(int startIndex)
{
for (int i = 1; i <= V; i++)
{
distances[i] = INF;
}
// 2. 출발 노드를 기준으로 각 노드의 최소 비용을 세팅
for (int i = 0; i < graph[startIndex].size(); i++)
{
int vertex = graph[startIndex][i].second;
int cost = graph[startIndex][i].first;
distances[vertex] = cost;
}
distances[startIndex] = 0;
visit[startIndex] = true;
for (int i = 1; i <= V-1; i++)
{
// 3. 방문하지 않는 노드 중 가장 cost가 적은 노드 선택.
int current = GetSmallIndex();
visit[current] = true;
// 4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신.
// 현재 연결된 노드중 가장 낮은 cost를 갖는 노드의 연결된 노드들을 확인
for (int j = 0; j < graph[current].size(); j++)
{
int vertex = graph[current][j].second;
// distances[vertex] = 현재 기록된 최소 cost.
// graph[current][j].first = 현재 연결된 노드의 인접 노드의 cost
// 현재 기록된 최소 cost보다 (현재 연결된 노드에서 인접노드로 가기 위한 cost + 현재 노드까지 오기 위한 cost)가 크다면 cost 갱신해 주기
if (distances[vertex] > graph[current][j].first + distances[current])
distances[vertex] = graph[current][j].first + distances[current];
}
}
}
void Input()
{
cin >> V >> E;
for (int i = 0; i < E; i++)
{
int from;
int to;
int distance;
cin >> from >> to >> distance;
graph[from].push_back(make_pair(distance, to));
graph[to].push_back(make_pair(distance, from));
}
// 1. 출발 노드 세팅.
cin >> startIndex;
}
int main()
{
Input();
Dijkstra(startIndex);
for (int i = 1; i <= V; i++)
{
cout << distances[i] << " ";
}
return 0;
}
// input
/*
6 10
1 2 2
1 3 5
1 4 1
2 3 3
2 4 2
3 4 3
3 5 1
3 6 5
4 5 1
5 6 2
1
*/위코드는 다익스트라를 단순 구현 했을 경우예요.
하지만 이처럼 구현하게 되면
int GetSmallIndex()
{
int min = INF;
int index = 0;
for (int i = 1; i <= V; i++)
{
if (distances[i] < min && !visit[i])
{
min = distances[i];
index = i;
}
}
return index;
}
3. 방문하지 않는 노드 중 가장 cost가 적은 노드 선택 -> 과정에서 해당 부분처럼 간선이 없더라도 일단 모든 노드를 다 탐색하기에

시간 복잡도가 O(N^2)가 나와요. 이 말이 무슨 말이냐면 노드가 10000개고 간선이 2개밖에 없더라도 일단 코드는 10000*10000번 탐색을 하는 비효율 적인 코드예요.
#define INF 1000000000
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int V, E;
int startIndex;
vector <pair<int, int>> graph[7];
int distances[7];
void Dijkstra(int startIndex)
{
for (int i = 1; i <= V; i++)
{
distances[i] = INF;
}
distances[startIndex] = 0;
priority_queue<pair<int, int>> pq;
pq.push(make_pair(0, startIndex));
while (!pq.empty())
{
// 3. 방문하지 않는 노드 중 가장 cost가 적은 노드 선택.
int distance = -pq.top().first;
int current = pq.top().second;
pq.pop();
//최단 거리가 아닌 경우 스킵
if (distances[current] < distance) continue;
// 4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신.
// 현재 연결된 노드중 가장 낮은 cost를 갖는 노드의 연결된 노드들을 확인
for (int i = 0; i < graph[current].size(); i++)
{
// 선택된 노드를 인접 노드로 거쳐서 가는 비용
int nextDistance = distance + graph[current][i].first;
// 선택된 노드의 인접 노드
int next = graph[current][i].second;
// 기존의 최소 비용보다 더 저렴하다면 교체.
if (nextDistance < distances[next])
{
distances[next] = nextDistance;
// 방문할 수 있는 노드이므로 이노드들에서도 탐색 시작
pq.push(make_pair(-nextDistance, next));
}
}
}
}
void Input()
{
cin >> V >> E;
for (int i = 0; i < E; i++)
{
int from;
int to;
int distance;
cin >> from >> to >> distance;
graph[from].push_back(make_pair(distance, to));
graph[to].push_back(make_pair(distance, from));
}
// 1. 출발 노드 세팅.
cin >> startIndex;
}
int main()
{
Input();
Dijkstra(startIndex);
for (int i = 1; i <= V; i++)
{
cout << distances[i] << " ";
}
return 0;
}
// input
/*
6 10
1 2 2
1 3 5
1 4 1
2 3 3
2 4 2
3 4 3
3 5 1
3 6 5
4 5 1
5 6 2
1
*/그래서 이렇게 연결이 된 부분들만 검사하는 즉 정점에 비해 간선이 적은 경우에도 대항할 수 있는 코드로 구현이 가능해요. 이렇게 될 때 시간 복잡도는 O(N * log N)이 나온다고 해요. priority_queue를 이용한 이유는 cost가 적은 노드부터 꺼내서 탐색하기 위해서 cost값에 -를 넣어서 넣게되면 cost가 작은 노드들이 가장 큰 값으로 정렬이 되기 때문에 사용했어요.

참고자료 :
23. 다익스트라(Dijkstra) 알고리즘 : 네이버 블로그 (naver.com)
개인 공부 기록용 블로그예요.
오류나 틀린 부분이 있을 경우
언제든지 댓글 혹은 메일로 지적해 주세요!